선형 리스트란?
[자료구조] 선형 리스트 (Linear List)
● 선형 리스트 (Linear List) - 데이터를 논리적인 순서대로 메모리에 연속하여 저장하는 구현하는 방식 - 데이터의 논리적인 순서와 기억 장소에 저장되는 물리적 순서가 일치하는 구조다. - 배열
toward-the-future.tistory.com
연결 리스트란?
[자료구조] 연결 리스트 (Linked List)
● 연결 리스트 (Linked List) - 각 데이터에 저장되어 있는 다음 데이터의 주소에 의해 연결되는 방식 - 데이터의 물리적인 순서와 상관없이 포인터를 사용하여 논리적인 순서대로 연결하는 구조다
toward-the-future.tistory.com
● 트리 (Tree)
- 원소들 간에 1 : n 관계를 가지는 비선형 자료구조
- 원소들 간에 계층 관계를 가지는 계층형 자료구조
- 상위 원소에서 하위 원소로 내려가면서 확장되는 트리(나무)모양의 구조
● 트리의 용어
- 노드(Node) : 트리의 원소
- 간선(Edge) : 노드를 연결하는 선
# 노드가 N개인 트리는 항상 간선이 (N - 1)개
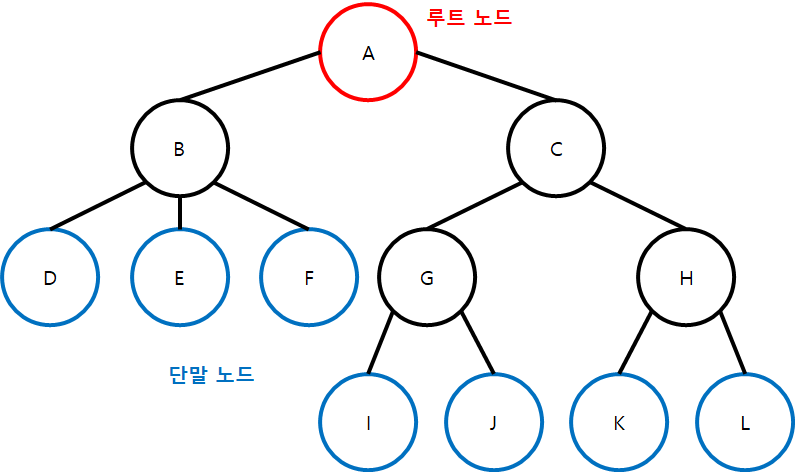
- 루트 노드(Root Node) : 트리의 시작 노드
- 단말 노드(Terminal Node) : 자식이 없는 노드, 가지가 더 이상 뻗어나갈 수 없는 마지막 노드, 리프 노드(Leaf Node)라고도 부른다.

- 부모 노드(Parent) : 어떤 노드와 간선으로 연결되었을 때 가장 위쪽에 있는 노드, 노드의 부모는 하나뿐이다.
- 자식 노드(Child) : 어떤 노드와 간선으로 연결되었을 때 가장 아래쪽에 있는 노드, 노드는 자식을 몇 개라도 가질 수 있다.
- 형제 노드(Sibling) : 부모가 같은 자식 노드
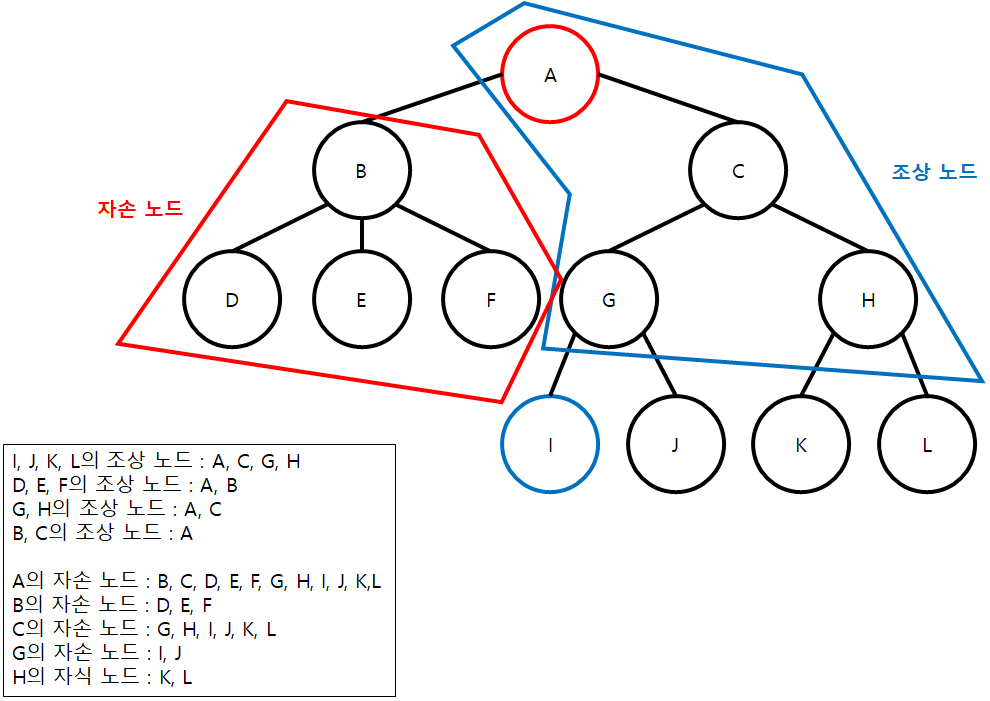
- 조상 노드(Ancestors) : 어떤 노드에서 위쪽으로 간선을 따라가면 만나는 모든 노드
- 자손 노드(Descendant) : 어떤 노드에서 아래쪽으로 간선을 따라가면 만나는 모든 노드

○ 차수(Degree)
- 노드의 차수 : 어떤 노드가 가지고 있는 자식의 수, 모든 노드의 차수가 n이하인 트리를 n진 트리라고 한다.
- 트리의 차수 : 트리에 있는 노드의 차수 중에서 가장 큰 값
○ 높이(Height) -> 깊이(Depth)라고도 부른다.
- 레벨 : 루트에서 어떤 노드에 이르는 간선의 수를 말한다.
- 노드의 높이 : 노드의 레벨
- 트리의 높이 : 트리에 있는 노드의 높이 중에서 가장 큰 값. 즉, 단말노드 레벨의 최댓값

- 서브 트리(Sub Tree) : 부모 노드와 연결된 간선을 끊었을 때 생기는 트리. 어떤 노드를 루트로 하고, 그 자손으로 구성된 트리. 즉, 큰 트리(전체)에 속하는 작은 트리이다.
- 포리스트(Forest) : 서브 트리의 집합
● 이진 트리 (Binary Tree)
- 트리를 구성하는 모든 노드들의 최대 차수가 2이하로 구성되는 트리이다.
- 노드가 왼쪽 자식 또는 오른쪽 자식만을 가질 수 있다. -> 부모 노드 : 자식 노드 = 1 : 2
- 이진 트리의 레벨 L에서 가질 수 있는 최대 노드의 수는 \((2^{L})\)개다.
- 높이가 h인 이진 트리가 가질 수 있는 노드의 개수는 최소 (h + 1)개이며, 최대 \((2^{h+1}-1)\)개
# 선형 리스트에서 이진 트리를 표현한 1차원 배열에서의 인덱스 관계
- 인덱스 0번은 실제로 사용하지 않고 비워둔다.
| 노드 | 인덱스 | 성립 조건 |
| 루트 노드 | 1 | n > 0 |
| 노드 i의 부모 노드 | i / 2 | i > 1 |
| 노드 i의 왼쪽 자식 노드 | 2 * i | (2 * i) <= n |
| 노드 i의 오른쪽 자식 노드 | (2 * i) + 1 | (2 * i + 1) <= n |
◎ 포화 이진 트리 (Perfect Binary Tree)
- 모든 레벨에 노드가 가득 차 있는 상태로 높이가 h일 때 최대 노드 수인 \(2^{h+1}-1\)개로 채워져 있는 트리
○ 선형 리스트를 이용한 포화 이진 트리

○ 연결 리스트를 이용한 포화 이진 트리

◎ 완전 이진 트리 (Complete Binary Tree)
- 마지막 레벨을 제외하고 모든 레벨에 노드가 가득 차 있는 상태로 마지막 레벨에서 왼쪽부터 오른쪽으로 노드가 채워져 있는 트리
○ 선형 리스트를 이용한 완전 이진 트리

○ 연결 리스트를 이용한 완전 이진 트리

◎ 편향 이진 트리 (Skewd Binary Tree)
- 모든 노드가 왼쪽이나 오른쪽 중 한 방향으로만 서브 트리를 가지고 있는 상태로 높이가 h일 때 최소 노드 수인 h + 1개로 채워져 있는 트리
○ 선형 리스트를 이용한 편향 이진 트리

○ 연결 리스트를 이용한 편향 이진 트리

● 이진 트리의 순회 (Tree Traverse)
| 전위 순회 (PreOrder) | 중위 순회 (InOrder) | 후위 순회 (PostOrder) |
| DLR (노드방문 -> 왼쪽 자식 -> 오른쪽 자식) |
LDR (왼쪽 자식 -> 노드방문 -> 오른쪽 자식) |
LRD (왼쪽 자식 -> 오른쪽 자식 -> 노드방문) |
 |
 |
 |

'Study > Data Structure' 카테고리의 다른 글
| [자료구조] 힙(Heap)과 우선순위 큐(Priority Queue) (0) | 2021.07.05 |
|---|---|
| [자료 구조] 2. 트리(Tree) - 이진 탐색 트리(Binary Search Tree), 균형 이진 탐색 트리(Balanced Binary Search Tree, AVL 트리) (0) | 2021.07.01 |
| [자료구조] 큐(Queue) - 선형 큐(Linear Queue), 원형 큐(Circular Queue), 연결 큐(Linked List Queue), 데크(Double-Ended Queue) (0) | 2021.06.29 |
| [자료구조] 스택(Stack) (0) | 2021.06.29 |
| [자료구조] 연결 리스트 (Linked List) (0) | 2021.06.28 |




댓글