선형 리스트란?
[자료구조] 선형 리스트 (Linear List)
● 선형 리스트 (Linear List) - 데이터를 논리적인 순서대로 메모리에 연속하여 저장하는 구현하는 방식 - 데이터의 논리적인 순서와 기억 장소에 저장되는 물리적 순서가 일치하는 구조다. - 배열
toward-the-future.tistory.com
연결 리스트란?
[자료구조] 연결 리스트 (Linked List)
● 연결 리스트 (Linked List) - 각 데이터에 저장되어 있는 다음 데이터의 주소에 의해 연결되는 방식 - 데이터의 물리적인 순서와 상관없이 포인터를 사용하여 논리적인 순서대로 연결하는 구조다
toward-the-future.tistory.com
스택이란?
[자료구조] 스택(Stack)
선형 리스트란? [자료구조] 선형 리스트 (Linear List) ● 선형 리스트 (Linear List) - 데이터를 논리적인 순서대로 메모리에 연속하여 저장하는 구현하는 방식 - 데이터의 논리적인 순서와 기억 장소에
toward-the-future.tistory.com
큐란?
[자료구조] 큐(Queue) - 선형 큐(Linear Queue), 원형 큐(Circular Queue), 연결 큐(Linked List Queue), 데크(Double-E
선형 리스트란? [자료구조] 선형 리스트 (Linear List) ● 선형 리스트 (Linear List) - 데이터를 논리적인 순서대로 메모리에 연속하여 저장하는 구현하는 방식 - 데이터의 논리적인 순서와 기억 장소에
toward-the-future.tistory.com
● 그래프 (Graph)
- 원소 들 간에 m : n 관계를 가지는 비선형 자료구조
- 그래프는 객체를 나타내는 정점(Vertex)과 객체를 연결하는 간선(Edge)의 집합으로 구성된다.
- G=(V, E)로 정의하는데, V는 그래프에 있는 정점의 집합이고, E는 정점을 연결하는 간선의 집합이다.
- 그래프 G의 정점의 집합은 V(G)로, 간선의 집합은 E(G)로 표현한다.
● 그래프의 종류
○ 무방향 그래프(UnDirected Graph) VS 방향 그래프(Directed Graph)

| 무방향 그래프 | 방향 그래프 |
| 두 정점을 연결하는 간선에 방향이 없는 그래프 | 두 정점을 연결하는 간선에 방향이 있는 그래프 |
| 정점 Vi와 Vj를 연결하는 간선을 (Vi, Vj)로 표현한다. # (Vi, Vj)와 (Vj, Vi)는 같은 간선이다. |
정점 Vi에서 정점 Vj를 연결하는 간선을 <Vi, Vj>로 표현한다. # <Vi, Vj>와 <Vj, Vi>는 다른 간선이다. |
| V(G) = {A, B, C, D} E(G) = {(A, B), (B, C), (C, D)} |
V(G) = {A, B, C, D} E(G) = {<A, C>, <B, A>, <C, D>, <D, B>} |
○ 완전 그래프 (Complete Graph)

- 각 정점에서 모든 정점이 간선으로 연결되어 있는 그래프이다.
- 정점이 n개인 무방향 그래프에서 최대 간선 수 : \(n(n-1)/2\)
- 정점이 n개인 방향 그래프에서 최대 간선 수 : \(n(n-1)\)
○ 부분 그래프 (Sub Graph)
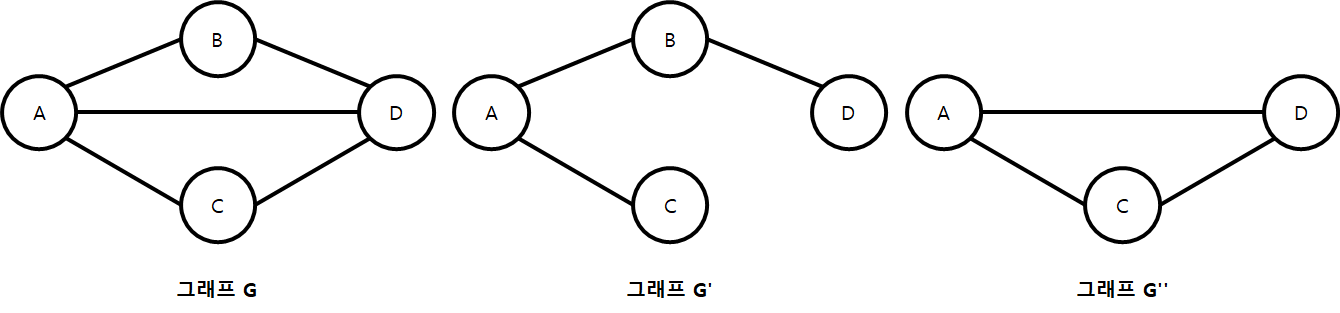
- 원래의 그래프에서 정점이나 간선을 일부만 제거하여 만든 그래프이다.
- 그래프 G와 부분 그래프 G'의 관계는 V(G') ⊆ V(G), E(G') ⊆ E(G)가 성립한다.
○ 가중치 그래프 (Weight Graph)

- 정점을 연결하는 간선에 가중치(Weight)를 할당한 그래프이다.
- 가중치(Weight)는 두 정점 사이의 거리 or 두 정점을 이동하는데 걸리는 시간과 같은 정보로 사용된다.
● 그래프의 용어
- 정점(Vertex) : 그래프의 원소
- 간선(Edge) : 정점을 연결하는 선
- 인접 정점(Adjacent Vetex) : 두 정점이 간선으로 연결되어있다면 두 정점은 인접하다고 할 수 있다.

○ 차수(Degree)
- 차수(Degree) : 무방향 그래프에서 정점에 연결되 간선의 수
- 진출 차수(Out-Degree) : 방향 그래프에서 외부에서 정점으로 들어오는 간선의 수
- 진입 차수(In-Degree) : 방향 그래프에서 정점에서 외부로 나가는 간선의 수

- 경로(Path) : 정점 Vi에서 정점 Vj로 가는 길
- 단순 경로(Simple Path) : 모두 다른 정점으로 구성된 경로
- 사이클(Cycle) : 단순 경로 중에서 경로의 시작 정점과 마지막 정점이 같은 경로
- DAG(Directed Acyclic Graph) : 방향 그래프이면서 사이클이 없는 그래프
● 인접 행렬(Adjacent Matrix)를 이용한 그래프
- 그래프의 두 정점을 연결한 간선의 유무를 선형리스트로 저장한다.
- n개의 정점을 가진 그래프는 2차원 배열의 n x n 정방 행렬로 저장한다.
- 행렬의 행 번호와 열 번호는 그래프의 정점이다.
- 행렬에는 두 정점이 인접되어 있으면 1, 인접되어있지 않으면 0을 저장한다.

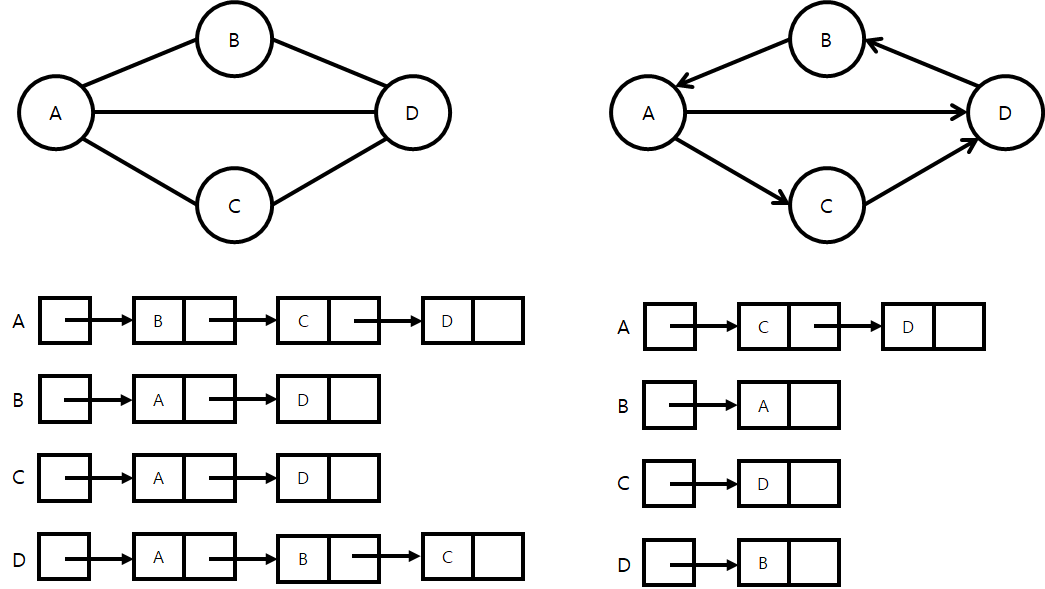
● 인접 리스트(Adjacent List)를 이용한 그래프
- 그래프의 두 정점을 연결한 간선의 유무를 연결 리스트로 저장한다.
- 리스트 내의 노드들은 각 정점의 차수만큼 인접 정점에 대해서 오름차순으로 노드를 연결한다.
● 그래프 순회 (Graph Traversal), 그래프 탐색 (Graph Search)
- 하나의 정점에서 시작하여 그래프에 있는 모든 정점을 한 번씩 방문하는 것이다.
○ 깊이 우선 탐색 (Depth First Search : DFS)
- 시작 정점을 정하고, 시작 정점에서 출발하여 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법
- 최대한 깊이 내려가다가 더 이상 갈 곳이 없으면 옆으로 이동한다.
- 더 이상 갈 곳이 없을 때 옆으로 이동하기 위해 '스택'을 사용한다.




○ 너비 우선 탐색 (Breadth First Search : BFS)
- 시작 정점을 정하고, 시작 정점에서 출발하여 인접한 노드를 먼저 탐색하는 방법
- 최대한 넓게 이동하다가 더 이상 갈 곳이 없으면 아래로 이동한다.
- 더 이상 갈 곳이 없을 때 아래로 이동하기 위해 '큐'를 사용한다.








댓글